廣町佐智子先生の看護研究の進め方第19回
廣町佐智子先生の看護研究の進め方⑲ 量的分析2
投稿日:2012.10.05
第5回「研究計画作成①」で、「研究は何を明らかにしたい内容によって、4つのパターンに分けられる」ことを説明しました。
そして、「はじめに」の最後の部分に「シメ」として、「研究で何を明らかにしたいのかを明確に記述する必要性」について説明しました。
ここでは、初心に立ち返り、自分が明らかにしたいことをしっかりと念頭に置きながら、二次集計(研究の目的に沿った分析)をしていくことになります。
また、二次集計の過程で眼にする「有意確率」の考え方について解説します。
Ⅰ.二次集計の方法
ここでは、研究の4つのパターンのうち、「差のあるなし」や、「関係のあるなし」を確認する場合の集計を中心に説明します。
そして、「はじめに」の最後の部分に「シメ」として、「研究で何を明らかにしたいのかを明確に記述する必要性」について説明しました。
ここでは、初心に立ち返り、自分が明らかにしたいことをしっかりと念頭に置きながら、二次集計(研究の目的に沿った分析)をしていくことになります。
また、二次集計の過程で眼にする「有意確率」の考え方について解説します。
Ⅰ.二次集計の方法
ここでは、研究の4つのパターンのうち、「差のあるなし」や、「関係のあるなし」を確認する場合の集計を中心に説明します。
1 変数間の差のあるなしを確認したい
差のあるなしの確認(検定)は、扱う尺度によって色々な方法があります。
以下にいくつかの尺度の組み合わせと、対応する統計学的仮説検定の種類を挙げました。
以下にいくつかの尺度の組み合わせと、対応する統計学的仮説検定の種類を挙げました。

ここで大切なのは、統計学的仮説検定の選択を間違わないということです。
選択さえ間違わなければ、各検定方法の考え方や分析手順、結果の見方は共通することが多いです。
詳しく勉強したい人は、統計の成書も確認してみてください。
②変数間の関係のあるなしを確認したい
主に相関分析という方法を用います。これは、2つの尺度(間隔尺度・比尺度や、5段階以上に分かれている順序尺度同士)について、関係があるかどうかを調べる方法です。
相関分析を統計ソフトに指示すると、相関係数を算出してくれます。
相関係数は、2つの尺度のあいだの関係の強さを示すものです。
相関の強さは、以下の表を参考にして評価していきます。
選択さえ間違わなければ、各検定方法の考え方や分析手順、結果の見方は共通することが多いです。
詳しく勉強したい人は、統計の成書も確認してみてください。
②変数間の関係のあるなしを確認したい
主に相関分析という方法を用います。これは、2つの尺度(間隔尺度・比尺度や、5段階以上に分かれている順序尺度同士)について、関係があるかどうかを調べる方法です。
相関分析を統計ソフトに指示すると、相関係数を算出してくれます。
相関係数は、2つの尺度のあいだの関係の強さを示すものです。
相関の強さは、以下の表を参考にして評価していきます。

上の表は、相関係数を絶対値で示していますが、実際には相関係数は、+で出てくるものと、-で出てくるものがあります。
それぞれ関係の意味が異なります。+ででてくる場合は「正の相関がある」といいます。
これは、Aという尺度が増えるほど、Bという尺度が増えるという意味です。一方、-で出てくるものは、「負の相関がある」といいます。
これは、Aの尺度が増えるほど、Bの尺度が減る関係にあるということを示します。
Ⅱ.「有意確率」の考え方:統計学的仮説検定
次に、二次集計の統計学的仮説検定の結果に出てくる「有意確率(p値)」について解説します。
統計学的仮説検定の考え方に関わる部分ですので、しっかり学んでおきましょう。
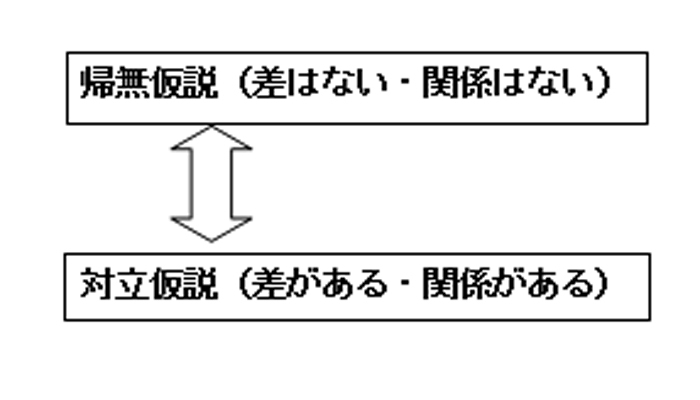
1)帰無仮説と対立仮説
統計学的仮説検定をする際には、まず仮説を立てます。皆さんが考える仮設は、普通、「差がある」とか「関係がある」という期待のこもったものになるでしょう。
しかし、「関係がある」「差がある」というのは、「ある」の程度が様々であいまいです。
一方、「関係がない」「差がない」というように、「ない」ことははっきりしているので、統計的に支持する確率を算出するのが簡単なのです。
そこで統計学的仮説検定では、あえて「関係はない」「差はない」という、研究者の意図とは逆の仮説、「帰無仮説」を立てます。
すると自動的に、帰無仮説とは反対の仮説である、「対立仮説」が設定されます。対立仮説は、帰無仮説を支持する確率が低かったときに支持される仮説なのです。
2)有意確率の見方
さて、話を有意確率に戻しましょう。
統計ソフトで統計学的仮説検定をすると、有意確率(P値)が出力されてきますが、これはまさに「帰無仮説を支持できる確率」のことをいうのです。
有意確率が低いと、帰無仮説は捨てられることになります。
では、どれくらい有意確率が低いと帰無仮説は捨てられるのでしょうか。
一般に5%以下の時です。このときに、「帰無仮説を支持できる確率はたった5%、5%間違う危険をおかして、対立仮説を支持する」と判断されます。
これを文章で表現すると、例えば「群間でBの割合、(or平均値)には有意な差があった(p<0.05)」とか、「AとBの間には有意な正の相関があった(r=0.335、p<0.05)」のようになります。
これらは、「5%の間違う危険性をおかして、群間でBの割合に差があることを支持する(群間の平均値に差があることを支持する、A・B間に相関があることを支持する)」という意味になるのです。
研究指導をしていると、データをあまり考えずに適当に収集してしまったために、二次集計、特に統計学的仮説検定ができないという事態にぶつかることがあります。
理想をいえば、研究計画の段階や、調査用紙の設計の段階で、得られたデータが検定などに耐えられるかどうか、統計に詳しい人に点検してもらうと良いでしょう。
そしてみなさんは、何も統計に詳しくなる必要はありません。検定の考え方や、データを判読するポイントを押さえておけば十分だと思います。
それぞれ関係の意味が異なります。+ででてくる場合は「正の相関がある」といいます。
これは、Aという尺度が増えるほど、Bという尺度が増えるという意味です。一方、-で出てくるものは、「負の相関がある」といいます。
これは、Aの尺度が増えるほど、Bの尺度が減る関係にあるということを示します。
Ⅱ.「有意確率」の考え方:統計学的仮説検定
次に、二次集計の統計学的仮説検定の結果に出てくる「有意確率(p値)」について解説します。
統計学的仮説検定の考え方に関わる部分ですので、しっかり学んでおきましょう。
1)帰無仮説と対立仮説
統計学的仮説検定をする際には、まず仮説を立てます。皆さんが考える仮設は、普通、「差がある」とか「関係がある」という期待のこもったものになるでしょう。
しかし、「関係がある」「差がある」というのは、「ある」の程度が様々であいまいです。
一方、「関係がない」「差がない」というように、「ない」ことははっきりしているので、統計的に支持する確率を算出するのが簡単なのです。
そこで統計学的仮説検定では、あえて「関係はない」「差はない」という、研究者の意図とは逆の仮説、「帰無仮説」を立てます。
すると自動的に、帰無仮説とは反対の仮説である、「対立仮説」が設定されます。対立仮説は、帰無仮説を支持する確率が低かったときに支持される仮説なのです。
2)有意確率の見方
さて、話を有意確率に戻しましょう。
統計ソフトで統計学的仮説検定をすると、有意確率(P値)が出力されてきますが、これはまさに「帰無仮説を支持できる確率」のことをいうのです。
有意確率が低いと、帰無仮説は捨てられることになります。
では、どれくらい有意確率が低いと帰無仮説は捨てられるのでしょうか。
一般に5%以下の時です。このときに、「帰無仮説を支持できる確率はたった5%、5%間違う危険をおかして、対立仮説を支持する」と判断されます。
これを文章で表現すると、例えば「群間でBの割合、(or平均値)には有意な差があった(p<0.05)」とか、「AとBの間には有意な正の相関があった(r=0.335、p<0.05)」のようになります。
これらは、「5%の間違う危険性をおかして、群間でBの割合に差があることを支持する(群間の平均値に差があることを支持する、A・B間に相関があることを支持する)」という意味になるのです。
研究指導をしていると、データをあまり考えずに適当に収集してしまったために、二次集計、特に統計学的仮説検定ができないという事態にぶつかることがあります。
理想をいえば、研究計画の段階や、調査用紙の設計の段階で、得られたデータが検定などに耐えられるかどうか、統計に詳しい人に点検してもらうと良いでしょう。
そしてみなさんは、何も統計に詳しくなる必要はありません。検定の考え方や、データを判読するポイントを押さえておけば十分だと思います。
◆看護研究の進め方◆
これであなたも即戦力!現場で役立つお役立ちコラム!
ケースレポートの書き方一覧
\ シェア /









